Représentation de Fresnel
Sommaire:
Objectifs:
- Représenter graphiquement une grandeur alternative sinusoïdale en utilisant la méthode Fresnel.
- Utiliser les lois fondamentales de l’électrotechnique pour déterminer une tension ou une intensité.
Mise en situation:
La valeur de la tension d’alimentation d’un moteur électrique fonctionnant en alternatif sinusoïdal monophasé est inscrite sur sa plaque signalétique.
- A quoi correspond la valeur indiquée ?
- Comment la mesurée ou la visualiser ?
- Comment modéliser cette tension
Représentation vectorielle:
https://phet.colorado.edu/sims/html/trig-tour/latest/trig-tour_fr.html Pour simplifier la représentation d’une tension sinusoïdale, on peut la modéliser par un vecteur tournant.
- Chaque valeur instantanée de la tension correspond à la projection du vecteur sur l’axe vertical.
- La période de la tension correspond au temps mis par le vecteur pour faire un tour.
- La fréquence correspond au nombre de tours effectués par le vecteur en 1 seconde.
| 360° = 2π (rad) |
Conversion degré en radian:
| angle en degré x 2π |
Conversion radian en degré:
| angle en radian x 360 |
La pulsation
- La pulsation correspond à l’angle en radian parcouru par le vecteur en 1 seconde.
- Elle se note ω et s’exprime en rad/s.
| ω = 2 x π x f |
Représentation vectorielle
Tout signal sinusoïdal peut être modélisé par un vecteur tournant appelé vecteur de Fresnel.
Le vecteur qui représente une tension se note
Un vecteur de Fresnel se caractérise par :
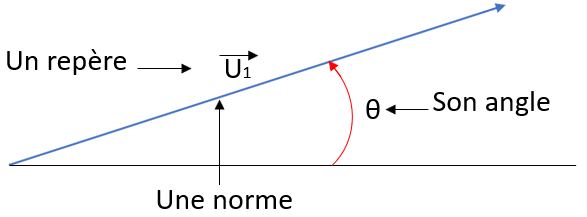
Equation mathématique d’une grandeur sinusoïdale
Tout signal sinusoïdal a une équation mathématique de la forme suivante :
| u(t) = U × √2 × sin(ωt + θ) |
- U= valeur efficace du signal (V)
- ω = pulsation du signal (rad/s)
- θ = phase à l’origine du signal (°)