Les Fonctions Logiques
Sommaire:
Fonction
En automatisme la valeur 1 est donnée pour symboliser un état actif (position travail) et la valeur 0
est associée à l’état repos.
Ce langage, ne comportant que 2 états possible s’appelle le langage binaire.
Les fonctions logiques sont un outils "Mathématique" utilisées dans les sciences de l'ingénieur pour
permettre de décrire le fonctionnement d'un système.
Elle sont extraite d'un règle connue sous le terme de "Algèbre de Boole".
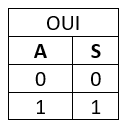
La Fonctions OUI
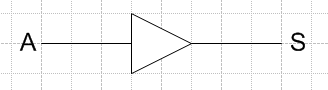
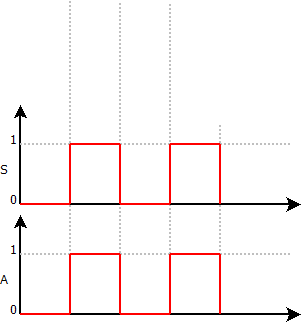
La fonction Oui permet l’enclenchement de la sortie lorsque l’entrée est valide.
Cette fonction est réalisée par l'utilisation d'un contact Normalement Ouvert (NO).
En électronique on parle aussi de la fonction buffer.
|
|
|
|

|
|
|
|
|
|
|
 |
|
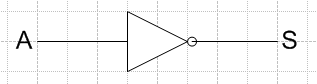
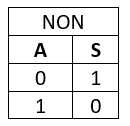
La Fonctions NON
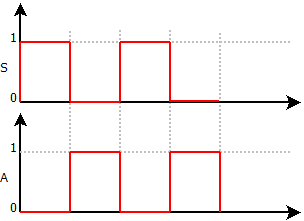
La fonction Non permet l’enclenchement de la sortie lorsque l’entrée n’est pas validée.
Elle repose sur l'utilisation d'un contact Normalement Fermé (NC).
|
|
|
|
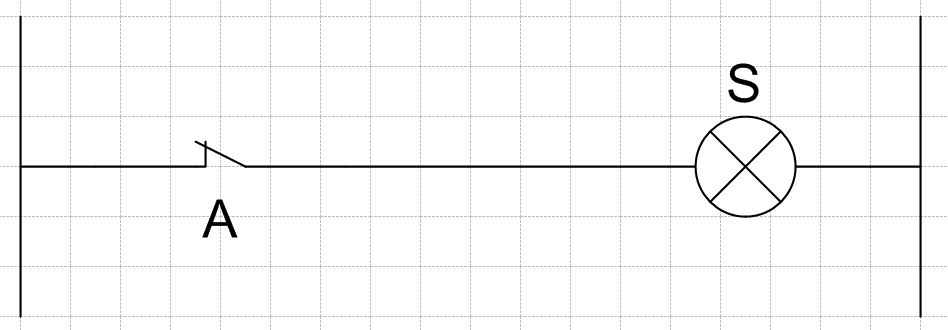
|
|
|
|
|
|
|
|
|
| S = |
| A |
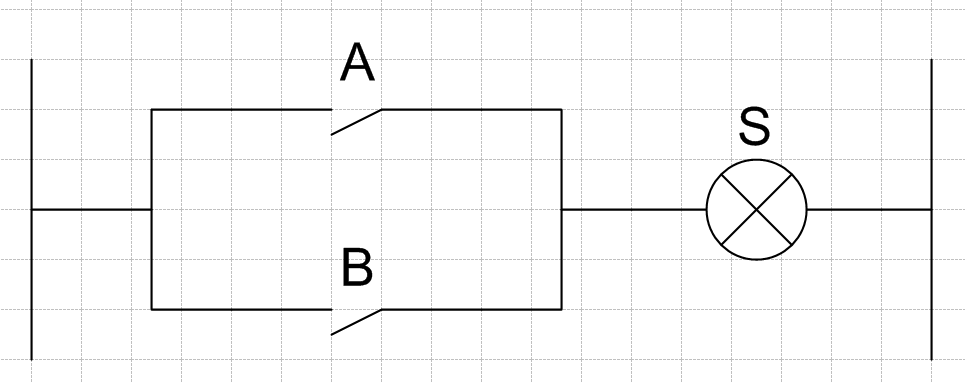
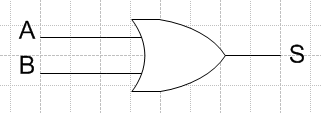
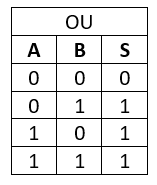
La Fonctions OU
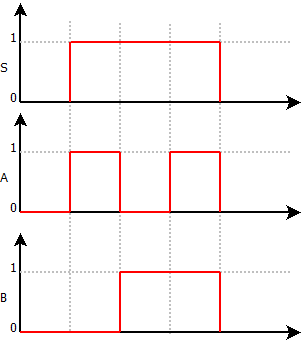
La fonction Ou permet l’enclenchement de la sortie lorsque l’une ou l’autre des entrées est validée.
On appelle souvent la fonction Ou la somme logique et se représente par un +.
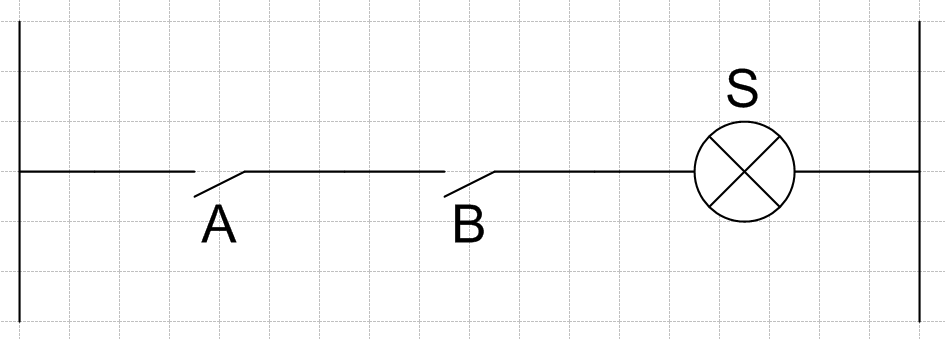
La fonction OU revient à câbler les différentes variable en dérivation.
| S = | ||
| A | + | B |
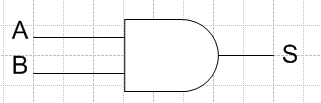
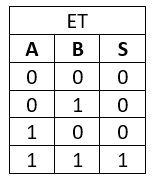
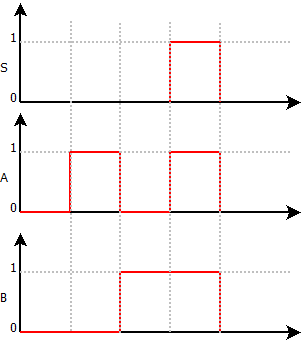
La Fonctions ET
La fonction ET permet l’enclenchement de la sortie lorsque toutes les entrées sont validées.
On appelle souvent la fonction ET, le produit logique et se représente par un * ou un . .
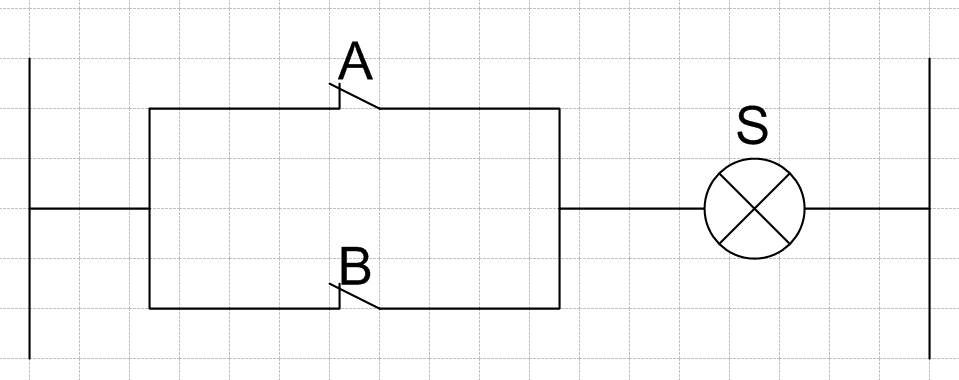
La fonction ET consiste à câbler en série les différentes variables.
| S = | ||
| A | . | B |
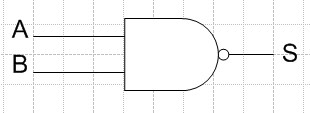
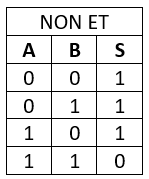
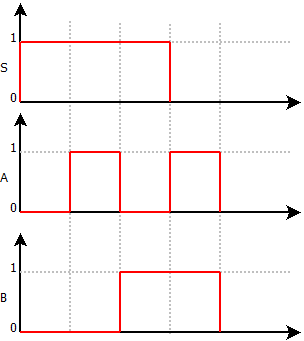
La Fonctions NON ET
La fonction ET NON (Nand) permet l’enclenchement de la sortie lorsque au moins une entrée n’est pas validée.
On dit pour une fonction Nand que 1 zéro en entrée force la sortie à 1.
| S = | ||||
| A.B | = | A | + | B |
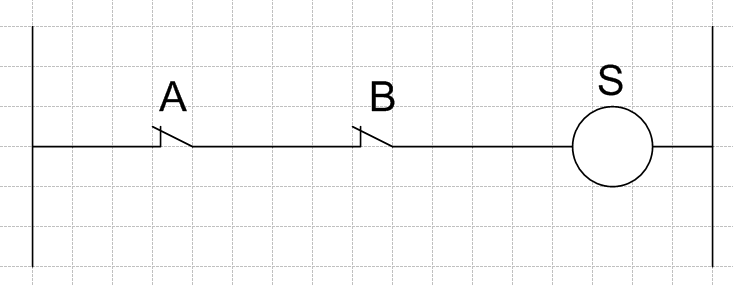
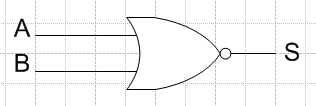
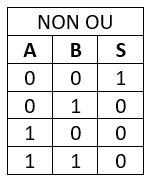
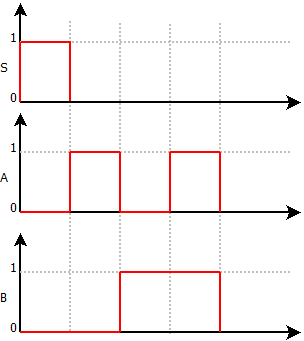
La Fonctions NON OU
La fonction NON OU (Nor) permet l’enclenchement de la sortie lorsque toutes les entrées ne sont pas validées.
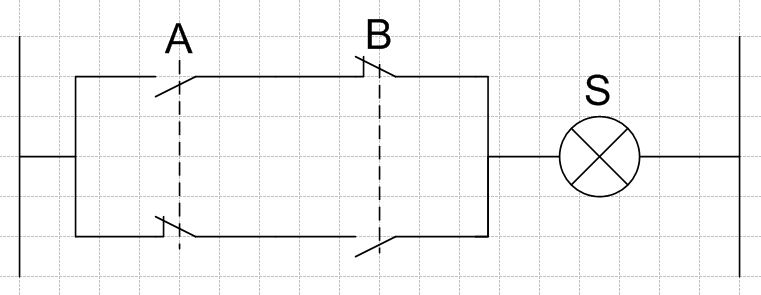
C'est l'architecture couramment utilisée pour les boucles de sécurité.
Si un arrêt (Normal ou Urgence) ou une capteur de sécurité est actif alors cela provoque l’arrêt du système.
| S = | ||||
| A+B | = | A | . | B |
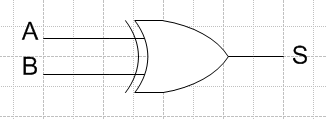
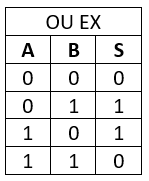
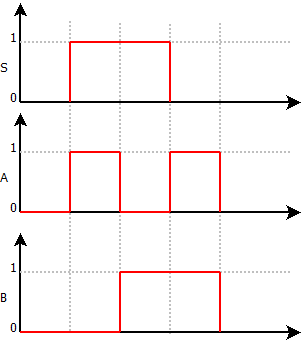
La Fonctions OU_EXCLUSIVE
La fonction OU Exclusif (Xor) permet l’enclenchement de la sortie lorsque les entrées sont dans un état opposé l’une de l’autre.
On retrouve cette fonction dans la commande de moteur 2 sens de rotation ou dans la commande de couplage étoile/triangle.
| S = |
| A⊕B |
Théoreme de De Morgan
Le théorème de De MORGAN s'exprime par les deux relations :
Les régles d'exécution
Permutativité
Les opérandes des fonctions logique peuvent etre permutées.
Cette régle est identique à la somme et au produit en arithmétique.
| A . B = B . A |
| A + B = B + A |
Parenthése et priorité
Comme en aritmétique, une équation logique se lit de gauche à droite.
Par contre les fonctions logique n'ont pas le meme degré de priorité.
Le produid logique (Fonction ET) est prioritaire sur la somme logique (Fonction OU).
Ainsi l'equation:
Pour permettre de modifié l'ordre de priorité, on utilisera des parenthéses.
Distributivité
Comme en mathématique, il est possible de développer ou de factoriser des équations logique:
A . (B + C) = A . B + A . C